油价算法机制是什么意思_油价的计算公式

1.我想知道队列算法能干什么

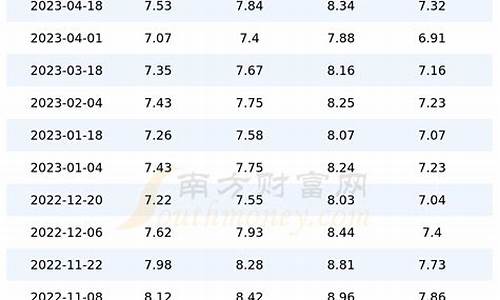
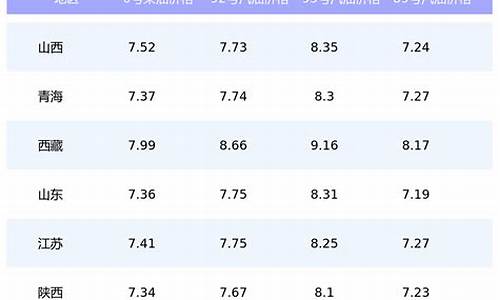
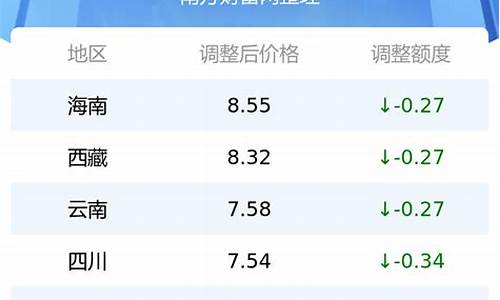
1、计算方式通常有几种，第一种是比较不精确的。是以车辆百公里油耗作为计算基准的。我们设您使用95号汽油，设目前95号汽油价格为每公升7元，那么100公里消耗掉8L汽油，一共就是56元油费。平均到每1公里就是0.56元人民币。我们可以按照这个计算方式，根据当前实际油价计算出车辆每1公里需要耗费多少油钱。

2、当然还有一个非常精准的油耗计算方法，就是一箱汽油完全消耗完，等到亮灯后用油耗计算软件记录里程数。然后加满一箱油之后一直跑到下一次亮灯，再记录一次里程数，按照加油量的多少，就能准确计算出实际油耗了。

我想知道队列算法能干什么

油耗的计算为：油耗x油价/100公里。百公里8.5升，按照7块钱一升来算，那么大概需要?60，也就是说每公里六毛钱左右。

设油箱红灯亮了去加油，加的是92号汽油，单价是6.2元/L，加满后总共用了300块（这里不讲你油箱多少L）。然后你归零公里数，从0公里开始算，等到下次红灯再亮时去加油。此时车子显示你一共跑了 480公里，加了290元，那么我们就得到数据290元跑了480公里。

百公里油耗，就是290元/480公里=0.6 0.6*100=60 60/6.2（油的单价）=9.67L 。

每公里就是290元/480公里=0.6。

每个人的车型不同，性能不同，油耗自然就会不一样，但是算法都是一样的，只要记住初始里程数和结束里程数，就能够算出自己车辆的油耗，但是往往这个实际油耗会比官方给出的油耗要高出一部分。

因为官方给出的数据都是理想状态的，比如一个驾驶员按照一定速度行驶一百公里的油耗，由于多数车辆在90公里/小时接近经济车速，所以大多数官方给出的油耗都是90公里/小时的百公里油耗，这完全就是理想状态。

百度百科-油耗

队列是一种先进先出的数据结构，由于这一规则的限制，使得队列有区别于栈等别的数据结构。

作为一种常用的数据结构，同栈一样，是有着丰富的现实背景的。以下是几个典型的例子。

[例5-2] 一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(设出发时油箱是空的).给定两个城市之间的距离D1,汽车油箱的容量C(以升为单位),每升汽油能行驶的距离D2,出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di,每升汽油价格Pi(i=1,2,……N).

计算结果四舍五入至小数点后两位.

如果无法到达目的地,则输出"No Solution".

样例:

INPUT

D1=275.6 C=11.9 D2=27.4 P=2.8 N=2

油站号I

离出发点的距离Di

每升汽油价格Pi

1

102.0

2.9

2

220.0

2.2

OUTPUT

26.95(该数据表示最小费用)

[问题分析]

看到这道题,许多人都马上判断出穷举是不可行的,因为数据都是以实数的形式给出的.但是,不用穷举,有什么方法是更好的呢 递推是另一条常见的思路,但是具体方法不甚明朗.

既然没有现成的思路可循,那么先分析一下问题不失为一个好办法.由于汽车是由始向终单向开的,我们最大的麻烦就是无法预知汽车以后对汽油的需求及油价变动;换句话说,前面所买的多余的油只有开到后面才会被发觉.

提出问题是解决的开始.为了着手解决遇到的困难,取得最优方案,那就必须做到两点,即只为用过的汽油付钱;并且只买最便宜的油.如果在以后的行程中发现先前的某些油是不必要的,或是买贵了,我们就会说:"还不如当初不买."由这一个想法,我们可以得到某种启示:设我们在每个站都买了足够多的油,然后在行程中逐步发现哪些油是不必要的,以此修改我们先前的购买,节省资金;进一步说,如果把在各个站加上的油标记为不同的类别,我们只要在用时用那些最便宜的油并为它们付钱,其余的油要么是太贵,要么是多余的,在最终的中会被排除.要注意的是,这里的便宜是对于某一段路程而言的,而不是全程.

[算法设计]由此,我们得到如下算法:从起点起(包括起点),每到一个站都把油箱加满(终点除外);每经过两站之间的距离,都按照从便宜到贵的顺序使用油箱中的油,并计算花费,因为这是在最优方案下不得不用的油;如果当前站的油价低于油箱中仍保存的油价,则说明以前的购买是不够明智的,其效果一定不如购买当前加油站的油,所以,明智的选择是用本站的油代替以前购买的高价油,留待以后使用,由于我们不是真的开车,也没有为备用的油付过钱,因而这样的反悔是可行的;当我们开到终点时,意味着路上的费用已经得到,此时剩余的油就没有用了,可以忽略.

数据结构用一个队列:存放由便宜到贵的各种油,一个头指针指向当前应当使用的油(最便宜的油),尾指针指向当前可能被替换的油(最贵的油).在一路用一路补充的过程中同步修改数据,求得最优方案.

注意:每到一站都要将油加满,以确保在有解的情况下能走完全程.并设出发前油箱里装满了比出发点贵的油,将出发点也看成一站,则程序循环执行换油,用油的操作,直到到达终点站为止.

本题的一个难点在于认识到油箱中油的可更换性,在这里,突破现实生活中的思维模式显得十分重要.

[程序清单]

program ex5_2(input,output);

const max=1000;

type recordtype=record price,content:real end;

var i,j,n,point,tail:longint;

content,change,distance2,money,use:real;

price,distance,consume:array[0..max] of real;

oil:array [0..max] of recordtype;

begin

write('Input DI,C,D2,P:'); readln(distance[0],content,distance2,price[0]);

write('Input N:'); readln(n); distance[n+1]:=distance[0];

for i:=1 to n do

begin

write('Input D[',i,'],','P[',i,']:');

readln(distance[i],price[i])

end;

distance[0]:=0;

for i:=n downto 0 do consume[i]:=(distance[i+1]-distance[i])/distance2;

for i:=0 to n do

if consume[i]>content then

begin writeln('No Solution'); halt end;

money:=0; tail:=1; change:=0;

oil[tail].price:=price[0]*2; oil[tail].content:=content;

for i:=0 to n do

begin

point:=tail;

while (point>=1) and (oil[point].price>=price[i]) do

begin

change:=change+oil[point].content;

point:=point-1

end;

tail:=point+1;

oil[tail].price:=price[i];

oil[tail].content:=change;

use:=consume[i]; point:=1;

while (use>1e-6) and (point=oil[point].content

then begin use:=use-oil[point].content;

money:=money+oil[point].content*oil[point].price;

point:=point+1 end

else begin oil[point].content:=oil[point].content-use;

money:=money+use*oil[point].price;

use:=0 end;

for j:=point to tail do oil[j-point+1]:=oil[j];

tail:=tail-point+1;

change:=consume[i]

end;

writeln(money:0:2)

end.

[例5-3] 分油问题:设有大小不等的3个无刻度的油桶,分别能够存满,X,Y,Z公升油(例如X=80,Y=50,Z=30).初始时,第一个油桶盛满油,第二,三个油桶为空.编程寻找一种最少步骤的分油方式,在某一个油桶上分出targ升油(例如targ=40).若找到解,则将分油方法打印出来;否则打印信息"UNABLE"等字样,表示问题无解.

[问题分析] 这是一个利用队列方法解决分油问题的程序.分油过程中,由于油桶上没有刻度,只能将油桶倒满或者倒空.三个油桶盛满油的总量始终等于开始时的第一个油桶盛满的油量.

[算法设计] 分油程序的算法主要是,每次判断当前油桶是不是可以倒出油,以及其他某个油桶是不是可以倒进油.如果满足以上条件,那么当前油桶的油或全部倒出,或将另一油桶倒满,针对两种不同的情况作不同的处理.

程序中使用一个队列Q,记录每次分油时各个油桶的盛油量和倾倒轨迹有关信息,队列中只记录互不相同的盛油状态(各个油桶的盛油量),如果程序列举出倒油过程的所有不同的盛油状态,经考察全部状态后,未能分出TARG升油的情况,就确定这个倒油问题无解.队列Q通过指针front和rear实现倒油过程的控制.

[程序清单]

program ex5_3(input,output);

const maxn=5000;

type stationtype=array[1..3] of integer;

elementtype=record

station:stationtype;

out,into:1..3;

father:integer

end;

queuetype=array [1..maxn] of elementtype;

var current,born:elementtype;

q:queuetype;

full,w,w1:stationtype;

i,j,k,remain,targ,front,rear:integer;

found:boolean;

procedure addQ(var Q:queuetype;var rear:integer; n:integer; x:elementtype);

begin

if rear=n

then begin writeln('Queue full!'); halt end

else begin rear:=rear+1; Q[rear]:=x end

end;

procedure deleteQ(var Q:queuetype;var front:integer;rear,n:integer;var x:elementtype);

begin

if front=rear

then begin writeln('Queue empty!'); halt end

else begin front:=front+1; x:=Q[front] end

end;

function dup(w:stationtype;rear:integer):boolean;

var i:integer;

begin

i:=1;

while (i<=rear) and ((w[1]q[i].station[1]) or

(w[2]q[i].station[2]) or (w[3]q[i].station[3])) do i:=i+1;

if i0 then

begin

print(q[k].father);

if k>1 then write(q[k].out, ' TO ',q[k].into,' ')

else write(' ':8);

for i:=1 to 3 do write(q[k].station[i]:5);

writeln

end

end;

begin {Main program}

writeln('1: ','2: ','3: ','targ');

readln(full[1],full[2],full[3],targ);

found:=false;

front:=0; rear:=1;

q[1].station[1]:=full[1];

q[1].station[2]:=0;

q[1].station[3]:=0;

q[1].father:=0;

while (front begin

deleteQ(q,front,rear,maxn,current);

w:=current.station;

for i:=1 to 3 do

for j:=1 to 3 do

if (ij) and (w[i]>0) and (w[j]remain

then begin w1[j]:=full[j]; w1[i]:=w[i]-remain end

else begin w1[i]:=0; w1[j]:=w[j]+w[i] end;

if not(dup(w1,rear)) then

begin

born.station:=w1;

born.out:=i;

born.into:=j;

born.father:=front;

addQ(q,rear,maxn,born);

for k:=1 to 3 do

if w1[k]=targ then found:=true

end

end

end;

if not(found)

then writeln('Unable!')

else print(rear)

end.